Multicellularity, Development, and Reproduction

Learning Objectives

  1. Describe the physiological challenges of and explain the adaptations for large cell size and multicellularity
  2. Explain the roles of the five essential developmental processes in development of a multicellular organism
  3. Describe the major reproductive strategies of eukaryotes
  4. Explain the trade-offs between asexual and sexual reproduction, and predict which replication mode is more likely in different environmental conditions
  5. Compare and contrast the three types of life cycles of eukaryotes

Large Cells: Problems and Solutions

Size presents problems for cellular access to nutrients and elimination of waste. We’ll discuss three distinct but inter-related phenomena in this reading:

  1. Constraints on cell size
  2. Multicellularity: development and specialization
  3. Reproduction in eukaryotes

The information below was adapted from Khan Academy “Structure of a Cell” and OpenStax Biology 4.2. All Khan Academy content is available for free at www.khanacademy.org

Cells are small, and prokaryotic cells are usually smaller than eukaryotic cells. The prokaryotic cells typically range from 0.1 to 5.0 micrometers (μm) in diameter, and eukaryotic cells typically range from 10 to 100 μm. The figure below shows the sizes of prokaryotic, bacterial, and eukaryotic, plant and animal, cells as well as other molecules and organisms on a logarithmic scale. Each unit of increase in a logarithmic scale represents a 10-fold increase in the quantity being measured, so these are big size differences we’re talking about!

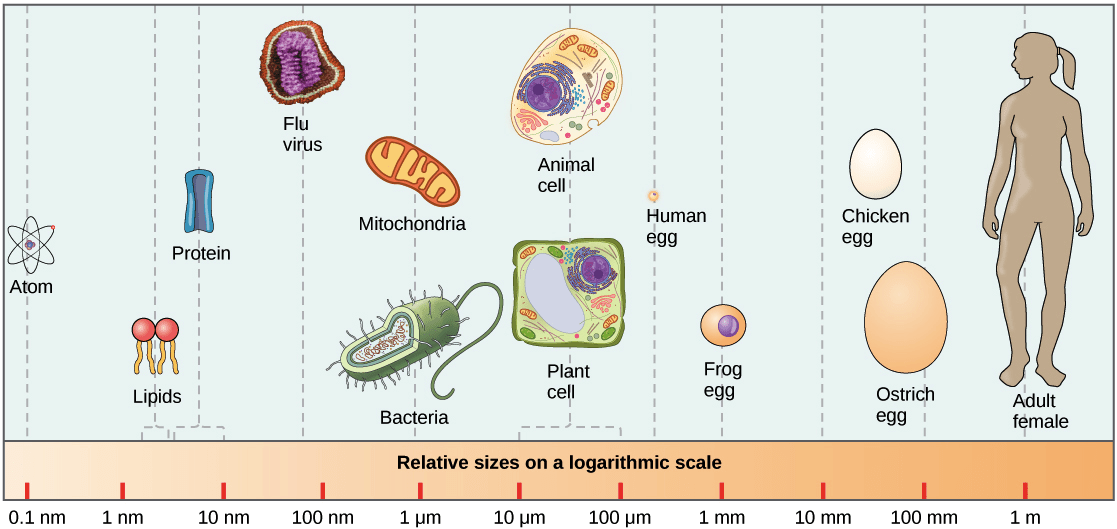
Relative sizes on a logarithmic scale, from 0.1 nm to 1 m, are shown (recall that each unit of increase in a logarithmic scale represents a 10-fold increase in the quantity being measured). Objects are shown from smallest to largest. The smallest object shown, an atom, is about 1 nm in size. The next largest objects shown are lipids and proteins; these molecules are between 1 and 10 nm. Bacteria are about 100 nm, and mitochondria are about 1 μm. Plant and animal cells are both between 10 and 100 μm. A human egg is between 100 μm and 1 mm. A frog egg is about 1 mm, A chicken egg and an ostrich egg are both between 10 and 100 mm, but an ostrich egg is larger. For comparison, a human is approximately 1 m tall.
Image credit: “Prokaryotic cells: Figure 2” by OpenStax College, Biology, CC BY 3.0

Small size, in general, is necessary for all cells, whether prokaryotic or eukaryotic. Why? Because cells rely on diffusion to bring nutrients in and eliminate wastes out. Diffusion speed of a particular nutrient or waste is relatively fixed; as cells become larger, it becomes more challenging for them to exchange enough nutrients and wastes with their environment. This challenge occurs both at the surface of the cell (moving molecules into or out of the cell) and also within the cell (moving molecules around within the cell).

To visualize this effect of cell size, let’s look at a cell’s surface-area-to-volume ratio. We will take an example of a cell shaped like a perfect sphere. (Not all cells are spherical in shape, but most tend to approximate a sphere.) The formula for the surface area of a sphere is 4πr2, while the formula for its volume is 4πr3/3. Thus, as the radius of a cell increases, its surface area increases as the square of its radius, but its volume increases as the cube of its radius; in other words, a cell’s volume increases much more rapidly than its surface area as it becomes larger. Therefore, as a cell increases in size, its surface area-to-volume ratio decreases. This same principle would apply if the cell had the shape of a cube, as in the figure below.

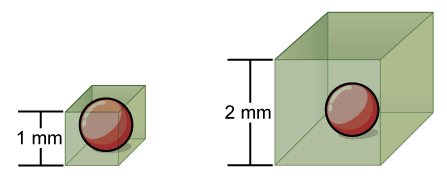
Notice that as a cell increases in size, its surface area-to-volume ratio decreases. When there is insufficient surface area to support a cell’s increasing volume, a cell will either divide or die. The cell on the left has a volume of 1 mm3 and a surface area of 6 mm2, with a surface area-to-volume ratio of 6 to 1, whereas the cell on the right has a volume of 8 mm3 and a surface area of 24 mm2, with a surface area-to-volume ratio of 3 to 1. Image credit: “Prokaryotic cells: Figure 3” by OpenStax College, Biology, CC BY 3.0

Why does a cell’s surface-area-to-volume ratio matter for cell size? There are two reasons: plasma membrane surface area and internal transport.

  • Plasma membrane surface area: The plasma membrane is the cell’s only interface with the environment. If the cell needs to take up nutrients or eliminate wastes, it must do so across the membrane. Each patch of membrane can exchange only so much of a given substance in a given period of time because it contains a limited number of channels. If the cell grows too large, its membrane will not have enough exchange capacity (surface area) to support the rate of exchange required for its increased metabolic activity (volume).
  • Internal transport: As cells get larger, it also takes longer to transport materials inside 0f them, because there is more distance that the material must cover before it gets to its destination within the cell.

The video below by provides an excellent visual demonstration of why diffusion matters with respect to cell surface area and cell volume:

The combination of these challenges place a general upper limit on cell size; however, eukaryotic cells are able to exceed prokaryotic cells due to their structural and metabolic features (for example, inner membranes and cytoskeletal elements). There are a number of evolutionary adaptations in response to the surface-area-to-volume problem and internal transport problem:

  • Cell geometry: Some cells are long and thin or have many protrusions from their surface, features that increase surface area relative to volume.
  • Reproduction: A cell can divide into two cells when it becomes too large to survive as one.
  • Internal complexity: Eukaryotic cells have internal organelles that compartmentalize and perform specific tasks; eukaryotic cells also contain internal “tracks” called cytoskeletons that can be used to transport materials at a rate faster than diffusion.
  • Multicellularity: A more complex solution is multicellularity, where an organism is made of multiple cells with specialized functions. The rest of this reading provides an overview of the requirements and consequences of multicellularity.

Multicellularity and Cell Specialization

The information below was adapted from OpenStax Biology 33.1

Multicellularity, or being composed of multiple cells, typically also requires cell specialization, where different cells carry out different functions from each other and often have different morphologies (shapes) optimized for carrying out those functions. For example, circulatory systems bring nutrients and remove waste, while respiratory systems provide oxygen for the cells and remove carbon dioxide from them. Other organ systems have developed further specialization of cells and tissues and efficiently control body functions. Moreover, surface-to-volume ratio applies to other areas of animal development, such as the relationship between muscle mass and cross-sectional surface area in supporting skeletons, and in the relationship between muscle mass and the generation of dissipation (loss) of heat.

The evolution of multicellularity and cell specialization resulted in a the requirement for development, or changes in an organism’s size, shape, and function during specific life stages. In the last portion of this reading, we’ll focus on the factors that influence and control development.

Five essential processes control development and specialization

How does a single cell (a fertilized egg) develop from one cell into many, each with different specialized functions? This process is called development, and it is regulated by five essential developmental processes:

  1. Cell proliferation: reproduction of new cells via mitosis; this process is critical for adding new cells (and thus mass) to body, making it larger
  2. Programmed cell death: death of specific cells; this process may seem like a bad thing, but certain cells actually have to die at certain stages for normal development. An example is human digits; during development, we have cells between our fingers which must die at precise times during development; otherwise, there would be webbing between our fingers.
  3. Cell movement or differential expansion: movement to new locations in the body (in animals) or differential expansion of cells in a specific direction (in plants); the process of gastrulation, which forms the gut, is the most dramatic example of cell movement in animals. Another interesting example is the movement of the testicular tissue from the abdomen to the scrotum in male development (testicles arise from the same tissue that creates ovaries in females).  Plant cells cannot move due to their cell wall, and instead differentially expand to cause the plant to bend.
  4. Induction: cell-cell communication or signaling; this process is critical for cells recognizing where they are in the body during development, and thus what type of cell they should become. Cell-cell communication can occur directly between immediately adjacent cells, or over long distances in concentration gradients.  Any signaling molecule that helps specify cell fate that is present in a concentration gradient is called a morphogen; the amount of morphogen a cell detects helps determine what that cell will become.
  5. Cell differentiation: the process of becoming a specific cell type, such as a bone cell or a muscle cell; this is often the final result of all the other processes, where an cell goes from an unspecified (embryonic) type to a final, specialized type of cell with a specific job in the organism.

The video below describes internal vs external factors (eg induction) that promote cell differentiation (specialization):

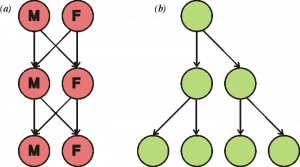
The timing of these developmental processes is highly regulated, and together result in development of specified tissue types and morphogenesis (development of an organism’s overall shape). The image below illustrates the relationships between three of these processes: cell proliferation (mitosis) results in creation of two identical daughter cells from one parent. Induction (cell-cell communication) from surrounding cells alters gene expression in these two genetically-identical cells, leading to cell differentiation into two distinct, specialized cell types.

Cell differentiation requires changes in gene expression in the differentiating cell. This differential gene expression leads to different cell types from a single parent cell.

Eukaryotic reproduction

The information below was adapted from OpenStax Biology 43.1

Development occurs following reproduction in multicellular eukaryotes. We’ll switch gears now to take an overview of reproductive processes in eukaryotes, including both sexual and asexual reproduction.

When organisms reproduce asexually, the offspring is an exact genetic copy of the parent. Asexual reproduction has a number of advantages over sexual reproduction including relative speed and low energy cost compared to finding and courting (attracting) a mate. There are a number of ways that some eukaryotic species reproduce asexually, including:

  • Mitosis: splitting into two (usually equal) halves (like binary fission, but with a nucleus; binary fission occurs in prokaryotes, while mitosis occurs in eukaryotes). All eukaryotes use mitosis, either to produce a new organism, or to produce new cells within a multicellular organism.
  • Multiple fission: splitting into more than 2 cells. Some fungi and some microbial eukaryotes reproduce through multiple fission.
  • Budding: outgrowth of a new cell from an old cell/new organism from old organism. Budding can occur when a single cell buds from a parent cell, or when multiple cells bud off of a larger organism. Budding occurs in some animal life stages (such as hydra in sea anemones, and the parasitic stage of flatworms) some fungi, and some microbial eukaryotes.
  • Fragmentation: mature organism splits into fragments capable of forming new organisms. Reproduction by fragmentation occurs in some fungi, some animals (such as starfish) and some plants.
  • Spores: specialized cells capable of forming a new organism; usually haploid and produced by meiosis. Reproduction by spores occurs in land plants and fungi.
  • Parthenogenesis: development of unfertilized egg into new organism. Parthenogenesis occurs in some animals (including some arthropods and some lizard species) and in some plants.
  • Polyembryony: fertilized egg splits to form genetically identical clones. Polyembryony can occur in some animals and some plants.
  • Vegetative growth: growth of new organism from meristematic cells without spores or gametes. Vegetative growth is a common reproductive strategy in plants.

Below are diagrams and pictures representing some of these forms of asexual reproduction:

Budding is a form of asexual reproduction that results from the outgrowth of a part of a cell or body region leading to a separation from the original organism into two individuals. Budding occurs commonly in some invertebrate animals such as corals and hydras. In hydras, a bud forms that develops into an adult and breaks away from the main body. Image credit: OpenStax Biology.
Sea stars can reproduce through fragmentation, breaking of the body into two parts with subsequent regeneration. The large arm, a fragment from another sea star, is developing into a new individual. Image credit: OpenStax Biology.
Stems allow for asexual reproduction by vegetative growth. (c) Ginger forms masses of stems called rhizomes that can give rise to multiple plants. (d) Each eye in the stem tuber of a potato can give rise to a new plant. (e) Strawberry plants form stolons: stems that grow at the soil surface or just below ground and can give rise to new plants. (credit: adapted from OpenStax Biology; c: modification of work by Albert Cahalan, USDA ARS; credit d: modification of work by Richard North; credit e: modification of work by Julie Magro)

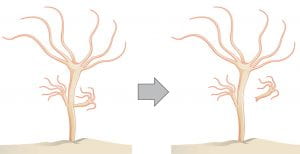
Sexual reproduction is the combination of (usually haploid) reproductive cells from two individuals to form a new (usually diploid) unique offspring. (For help and review with the the concept of ploidy, as well as mitosis and meiosis, see the Biological Principles textbook page on Cell Division.) Compared to asexual reproduction, sexual reproduction has several big disadvantages: it requires the time and energy to find a mate, and only half of the populations (females) can actually make offspring.  In contrast, because every member of an asexually-reproducing population can generate offspring, this means that, with all else equal, an asexually reproducing population will out-compete a sexually-reproducing population when in direct competition with each other.

This diagram illustrates the twofold cost of sex. If each individual were to contribute to the same number of offspring (two), (a) the sexual population remains the same size each generation, where the (b) asexual population doubles in size each generation. CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1599721

However, asexually-reproducing individuals can only make clones, meaning that each of their offspring are genetically identical (except in the case of mutations). A population of identical individuals can be a disadvantage if conditions suddenly change, and the individuals are no longer well-adapted to the conditions. In contrast, sexual reproduction produces offspring with novel combinations of genes, which can be an advantage in unstable or unpredictable environments.

Pros and Cons of Sexual and Asexual Reproduction

The information below was adapted from Wikipedia:

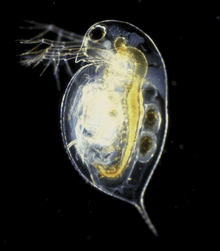
In some species, such as the water flea Daphnia pulex (shown below), individuals can switch between sexual and asexual (parthenogenic) reproduction. Daphnia live in various aquatic environments, including ponds, lakes, streams, and rivers. Early in the growth season, when food is abundant, diploid Daphnia females reproduce asexually via parthenogenesis. Almost all Daphnia in these populations are female and genetically identical to their mothers. Toward the end of the growing season, when conditions are not as stable or ideal, the Daphnia females alter their reproductive strategies to produce male as well as female offspring, as illustrated in the graph below. Instead of reproducing parthenogenic, diploid daughters, they begin producing haploid eggs which are then fertilized by the males. These special haploid eggs are capable of surviving extreme conditions such as cold or drought, and they will hatch into diploid individuals once environmental conditions improve.

Daphnia pulex. Image credit: Functional Genomics Thickens the Biological Plot. Gewin V, PLoS Biology Vol. 3/6/2005, e219. doi:10.1371/journal.pbio.0030219
As the population density increases, more Daphnia females reproduce sexually rather than asexually. Image based on data from Kleiven, Larsson, and Hoboek, 1992. Oikos 65: 197-206.

The two videos below discuss some of these considerations as they attempt to answer the questions of “why is sex a thing?”

Eukaryotic Life Cycles

Regardless of an organism’s ecology, there are three fundamental steps to sexual reproduction:

  • Gametogenesis: making gametes, which are typically called eggs and sperm
  • Mating: getting gametes together, which involves sperm and egg being released at the same time and location
  • Fertilization: fusing gametes into a single cell, which is then called a zygote

Life cycles: Different organisms accomplish these three steps in different ways and at different times in their life cycles (note that a change in ploidy is always required). All life cycles involve a haploid (1 complete set of chromosomes) and diploid (2 complete sets of chromosomes) stage, but they vary in how and when in the life cycle these stages occur.

In the diplontic life cycle, which is typical of animals, the mature, multicellular organism is diploid (2n). In the haplontic life cycle, which is typical of some algae, and fungi, the mature, multicellular organism is haploid. In the alternation of generations life cycle, which is typical of plants, there are two mature, multicellular organisms: one haploid, and one diploid.  These life cycles are illustrated below, with details about each life cycle provided in the captions. Before you read through the details of these diagrams, let’s define some terms:

  • Gamete: a mature haploid male or female germ cell that is able to unite with another of the opposite sex in sexual reproduction to form a zygote
  • Spore: a small, typically one-celled, reproductive unit capable of giving rise to a new individual without sexual fusion

Gametes are always haploid, and spores are usually haploid (spores are always haploid in all contexts we will consider in this class and in the diagrams below).

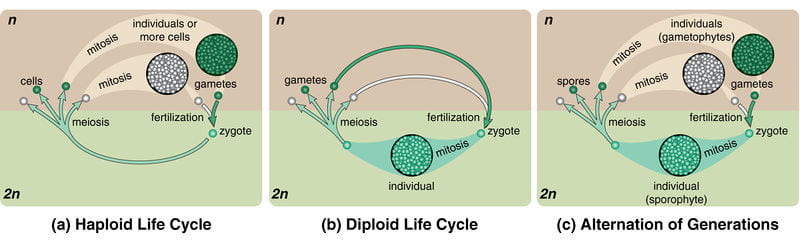
Eukaryotic Life Cycles
Eukaryotic life cycles. A: Haplontic life cycle. The mature, multicellular organism is haploid and produces haploid gametes via mitosis, which fuse into a diploid zygote. The zygote immediately undergoes meiosis to produce haploid spores, which develop into mature multicellular haploid individuals. B: Diplontic life cycle. The mature, multicellular organism is diploid and produces haploid gametes via meiosis, which fuse into a diploid zygote. The zygote undergoes development into a mature multicellular diploid organism. C: Alternation of Generations. There is a mature multicellular haploid stage and a mature multicellular diploid stage. The multicellular haploid stage (the gametophyte) produces gametes via mitosis which fuse to form a diploid zygote. The zygote develops into a mature multicellular diploid individual (the sporophyte), which produces haploid spores via meiosis. The haploid spores then develop into a mature multicellular haploid individual.. Image credit: CK-12 Foundation, https://www.ck12.org/book/biology-i-honors-(ca-dti3)/r1/section/6.2/

Alternation of generations is often the most confusing life cycle to understand, because it is so different from the diplontic life cycle (what we think of as “normal”.) The video below illustrates the differences between the diplontic and alternation of generations life cycles: